 |
 |
- Search
| Arch Hand Microsurg > Volume 26(4); 2021 > Article |
|
Abstract
Purpose
Various factors such as blood velocity, turbulent flow, and intimal injury are the most basic elements in free tissue transfers. However, how blood flow is reestablished, maintained, and changed after vascular anastomosis has rarely been studied.
Methods
A 54-year-old male sustained an unreplantable severe crushing injury to his right hand. The middle finger was transferred to the thumb as an ectopic replantation using an anastomosis between the radial and digital arteries. However, secondary reconstruction for the first web space defect was inevitable and an anteromedial thigh free flap procedure was performed 2 months later using the previously anastomosed vessels. During the procedures, we noted morphologic changes in the microvessels and tried to explain those phenomena by applying the principles of hemodynamics.
Results
ue to the discrepancy in vascular size between the radial and digital arteries, the velocity of the blood flow in the post-anastomotic site, which was the digital artery, must have been increased by Poiseuille’s law. Supposing that the velocity through the post-anastomotic site of the digital artery was increased, the pressure exerted by that flow decreased, resulting in more shrinkage of the vessel lumen of the digital artery by Bernoulli’s principle. Pascal’s law could also be applied in confined spaces with a static flow; where there is a constant pressure, as the radius of the post-anastomotic digital artery diminishes, the tension within the digital artery’s wall also simultaneously decreases. By Laplace’s law, the post-anastomotic digital artery’s wall thickens as less tension is exerted on the wall.
Although the success rate of free tissue transfer has been reported to be more than 95%, flap loss due to thrombosis of the vascular anastomosis is still a challenge for microsurgeons [1]. Therefore, in addition to an accurate anastomosis, maintaining adequate arterial pressure and cardiac output and good perfusion pressure to the flap are vital to perioperative flap survival [2].
Hemodynamic changes such as perioperative blood flow and velocity in free tissue transfers have been researched in many ways to improve vascular patency [3-11]. Understanding how blood flow is reestablished, maintained, and changed after vascular anastomosis is the most basic element in free tissue transfers. Postoperative inflammation and denervation cause vasodilation, resulting in increased blood flow in free tissue transfer. Furthermore, arterial occlusion after free tissue transfer has been infrequently reported beyond the critical period in flap survival and it may even occur as late as postoperative day 6 [12]. However, there has been no proper scientific, hemodynamic explanation of that devastating event including any significant change in the diameter of the anastomosed vessel.
Many seem to agree that the high discrepancy in vessel size affects the patency rate, increasing the occlusion of the anastomosis [13,14]. Blood flow turbulence in small vessels may be an important factor in thrombus formation as blood passes through different-sized vessel lumens. Monsivais [15] indicated that veins grafted to arteries at ratios of 0.75:1 and 1:1 yielded the highest patency rates without citing any theoretical basis.
Blood vessels are not rigid tubes, so classic hydrodynamics and fluids mechanics based on the use of classical viscometers are not capable of explaining the related hemodynamics [16]. Furthermore, blood flow, as a non-Newtonian fluid should be best studied using rheology rather than hydrodynamics. Nonetheless, considering that the blood flow in the microvessels is laminar with a steady flow, we borrowed some principles from physics to introduce an interesting clinical case in a free tissue transfer patient.
Through our presented case, we reviewed the basic hemodynamic principles, which have not been published in the literature yet. This review might help elucidate the microvascular changes in the created microvascular anastomosis.
A 54-year-old male patient sustained a severe crushing injury from a press machine to his right hand (Fig. 1A). The thumb and index finger were unreplantable and we transferred the middle finger to the thumb in an ectopic replantation. The digital artery from the radial side of the middle finger was anastomosed with the branch of the radial artery at the carpal level. The size discrepancy was overcome by making a beveled cut at the end of the digital artery (Fig. 2). The first web space and hand dorsum were covered by the fillet flap from the remnant tissues. Although the pollicized thumb survived, the adjacent soft tissues, which had been covered by the fillet flap from the spare part, were necrosed 2 months postoperatively (Fig. 1B). We debrided the necrotic tissues and planned to cover them with an anterolateral thigh free flap in consecutive procedures. However, due to his anatomical variations in the branches of the lateral femoral circumflex artery, an anteromedial thigh (AMT) flap was elevated and transferred to the right hand (Fig. 1C). While cutting the previously anastomosed site of the microvessels for the end-to-side anastomosis, we found a narrow lumen with a thickened arterial wall at the distal part of the previously anastomosed site (Fig. 3). Because this part was impossible to use for the end-to-side anastomosis of the AMT pedicle artery, we cut this portion of the thickened vascular wall area en bloc and inserted a vein graft from the lesser saphenous vein in a Y-shape (Fig. 1C). Postoperatively, the patient had an uneventful course without any complications such as infections, hematoma, dehiscence, and flap necrosis. The AMT flap had no congestion and survived completely and the patient was satisfied with the final functional result and grip (Fig. 1D).
Fluid presents as a form of liquid or gas and flows in two patterns, laminar or turbulent. Blood is a suspension of fluid consisting of various blood cells and plasma, with a viscosity greater than that of water. Its viscosity is affected by the speed, vessel size, and temperature of the blood flow. Normal blood plasma behaves like a Newtonian fluid at physiological shear rates. Therefore, we could safely apply various physical principles of fluid dynamics to hemodynamics.
Although laminar flow is the most efficient manner by which fluid moves, true laminar flow is rarely found in the arterial circulation but is observed in small vessels, especially those less than 5 mm in diameter [17]. Therefore, we supposed that the flow of the microvessels involved in free tissue transfers accords to laminar flow principles. Clinically, within a vessel, turbulent flow occurs when the rate of blood flow is too rapid or the blood flow passes over an affected surface. The transition from laminar to turbulent flow is determined by Reynolds number (Re), which is used to predict flow patterns in different fluid flow situations. Re represents the tendency for turbulence to occur [18,19].
Re=(v×d×p)/η
where v is the flow velocity, d is the diameter, p is the density of the fluid, and η is the dynamic viscosity.
When Re exceeds 200, turbulence will occur at the branching point and when Re is greater than 2,000, turbulent flow will occur even in the smooth portion of a given vessel [20]. For capillaries with very small diameters, Re is small and the flow becomes laminar [17]. At high Re, turbulence results from differences in the speed and direction of the fluid, which may sometimes produce eddy currents. Turbulence may occur at much lower Re in situations where the conduit wall is rough, such as intimal injury of the microvessels or a vascular prosthesis with a rough inner surface. In in vivo human arterial systems, intimal roughening and arteriosclerotic changes are known to cause blood flow turbulence even in relatively small arteries. In turbulence caused by sudden alterations in the direction such as in bifurcations, the velocity and magnitude of the flowing stream seem to be related to the thrombogenic tendency, resulting in flap failure. Venous stasis due to prolonged surgery or immobilization may also result in thrombi production by triggering anticoagulation pathways. Written informed consent was obtained for publication of this original article and accompanying images.
When we cut the previously anastomosed site, which had overcome the size discrepancy, we found that the pedicle artery was constricted and its wall was thickened too much to be appropriate for the secondary microvascular anastomosis (Fig. 3A). The adventitia was also found to be hard due to fibrotic changes.
Considering that the actual blood flow and vessel resistance are not steady and laminar, but dynamic and phasic, it is not entirely accurate to strictly apply fluid mechanics to the hemodynamics in free tissue transfer. Nonetheless, the knowledge of principles of hemodynamics may provide the mechanism of how the microvessels change after anastomosis in a human vascular system. In our presented clinical case, we noted the following physical principles of fluid dynamics, which explained the post-anastomotic microvascular changes.
In the human vascular system, the blood flow volume is mainly determined by the pressure differential and the resistance to vascular flow.
Blood flow volume=pressure difference (P1–P2)/resistance to flow (R)
It is regarded as Ohm’s law in the field of hemodynamics. This explanation could be expanded to the following Poiseuille’s law.
This principle explains the relationship between blood pressure, blood flow, and vascular resistance. The blood volume flowing through a vessel is directly proportional to the pressure drop along with the distance of the vessel (P1–P2) and the fourth power of the radius of the vessel and is inversely proportional to the length of the vessel (L) and the viscosity of the blood (η) (Fig. 4).
Volume flow rate (F)=pressure difference (P1–P2)/viscous resistance (R)
Therefore, in addition to the pressure difference, the diameter of the vessels seems to be the next most important factor in overall blood flow. Theoretically, this is only qualitatively applicable to human vessels with highly variable dimensions, elastic walls, a constantly changing pressure head, and containing a nonviscous fluid [10].
This law implies why we should prefer larger vessels during microsurgical free tissue transfers. Despite an accurate anastomosis of the microvessels, irregularities at the boundary surface might cause a loss of flow due to the eddy currents. A surface irregularity of a given size causes more friction in a tube of a small diameter than it does in a tube with a larger diameter.
The rate or velocity of blood flow varies inversely with the total cross-sectional area of the blood vessels. Assuming that the constant amount of flow is maintained, the velocity of the blood flow increases as it passes through narrower vascular lumens (Fig. 5). In the pulsatile arterioles, the principle can still be applied to the mean flow parameters.
Bernoulli’s principle implies a quantitative representation of the relationship between the flow and the pressure of a fluid. A good visualization of the Bernoulli effect is the flow through a constriction, assuming that the flow is visualized as an ideal laminar flow. When the blood flow speeds up in a constricted vessel area, its exerted pressure is decreased in that region (Fig. 6), assuming that the density is constant. Conversely, a decrease in blood velocity is associated with an increase in the exerted hydraulic pressure.
In this presented case, as the velocity of the blood flow increased in the post-anastomotic site of the digital artery, the hydraulic pressure exerted by that flow decreased, resulting in more shrinkage of the vessel lumen of the digital artery according to Bernoulli’s principle.
In fluid physics, the pressure applied to any part of the enclosed liquid will be transmitted equally in all directions throughout the liquid, resulting in the same changes everywhere. This is also applied to confined spaces with static, but continuous flow, which we use here to explain hemodynamics.
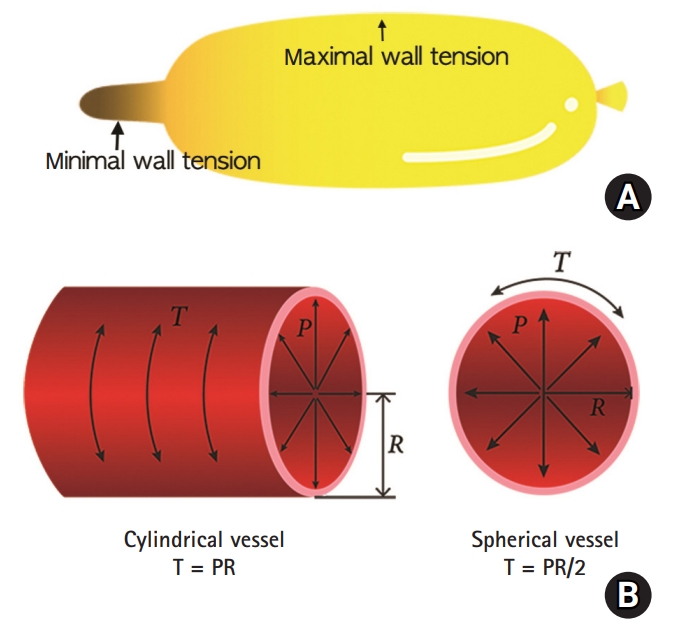
Laplace’s law was originally used to explain the pressure-volume relationship of spheres. The tension within the wall of a sphere filled to a particular pressure depends upon the thickness of the sphere. The wall tension is proportional to the sphere’s radius for a given exerted pressure (Fig. 7). This principle can also be applied to cylinder-shaped blood vessels. Assuming that the thickness of the vessel wall is very small compared to the diameter of the vessel lumen, its exerted pressure is related to the wall tension of the vessel.
where pressure is the pressure inside the sphere (or cylinder), thickness is the thickness of the sphere wall, and tension is the tension within the sphere wall.
According to Pascal’s law, in our presented case, the vascular anastomosis site tends to maintain a constant homeostatic pressure between the radial and digital arteries. Where there is a constant pressure, as the radius of the post-anastomotic digital artery diminished, the tension within the digital artery’s wall also simultaneously decreased (Fig. 7). Therefore, as we show in Fig. 7, illustrating Laplace’s law, the post-anastomotic digital arterial wall thickened more as the tension of the wall decreased.
The application of fluid dynamics to clinical fields has been performed mainly in the cardiovascular system and called “hemodynamics.” Many factors such as blood velocity, turbulence, and shear stress have implications on the blood flow within the closed systems of the blood vessels. Whether the same phenomena seen with the physical laws of fluid dynamics could be adjusted and applied to the hemodynamics of free tissue transfer sees impractical. However, beyond the cardiovascular system, del Zoppo [21] studied the effect of shear on the cerebral circulation in brain injury and Allan [22] cited Bernoulli’s principle in the mechanism of iris prolapse [23]. Recordati [24] proposed considering Bernoulli’s principle in hemodynamics using a giraffe’s neck model. Assuming that the flow in the microvessels is laminar, we also could apply the four physical principles; Poiseuille’s principle, Bernoulli’s principle, Pascal’s law, and Laplace’s law in fluid dynamics by observing the morphologic changes in the anastomosed microvessels of different calibers. Until now, no preconceived assumptions were made regarding our observations that might have been predicted on the basis of hydrodynamic laws.
Because free tissue transfer affects blood flow through the flap, many studies have been performed to reveal the changes in hemodynamic parameters and their effects on the outcome of free tissue transfer [7,25-33]. The patency of the microvascular anastomosis is affected by many factors such as the type of repair, the careful use of vasodilating agents, blood turbulence, the presence of endothelial injury at the repair site, size discrepancy, the graft length of the vessels, and various surgical techniques. Turbulence is certainly the important factor affecting the thrombus formation at the repair site, especially where any size discrepancy exists [15,34,35]. A high-velocity jet occurs just beyond the stenosis at which true turbulence is produced [17]. This produces eddy currents, which are slow and prone to promoting platelet deposition. We assume that this “post-stenotic turbulence” might be the major cause of the post-anastomotic failure of microvessels. Considering that brisk, laminar flow is minimally thrombogenic, it is important to make the correct apposition of the cut vessel edges smoothly in the microvessels.
It is generally agreed that the higher the existing diameter discrepancy, the lower the patency rates due to the risk of thrombosis [13]. Monsivais [15] suggested that the discrepancies in diameter should fall within a range of 0.75 to 1:1. Furthermore, a vein graft might change the caliber of the vessels, causing turbulence, which also might provide an additional thrombogenic stimulus [18]. However, there was no difference in the flap survival of vein-grafted free flaps [19]. In vein grafts, systemic heparinization and reductions in the longitudinal tension should be emphasized to improve graft patency. Regarding the vein graft length, much longer grafts may provide a chance for turbulent flow to dissipate and laminar flow to be reestablished. This might also affect the flow conditions at the distal anastomosis. However, other studies revealed that the length of venous autografts did not affect patency in microvascular anastomoses [23,36]. To obtain a maximal volume flow, the relative diameters of the graft should be about twice that of the artery [10]. However, this also might reduce the velocity of the flow, resulting in vascular thrombosis according to Poiseuille’s law. Therefore, Szilagyi et al. [10] suggested a diameter ratio of 1:1.4 to 1:1.6 between the proximal artery and the graft for technical ease and hemodynamic efficiency.
In the field of microsurgical reconstruction, thrombosis at the post-anastomotic site is a major factor in the failure of free tissue transfers. Although vascular thrombosis mostly occurs within the first 3 postoperative days, late thrombosis jeopardizing free flap survival has been infrequently reported [9,37,38]. Salgado et al. [37] described the late loss of arterial inflow to the free flap at an average of 54 days postoperatively and partial flap loss after arterial disruption on postoperative day 100. However, there were no definite explanations for those flap failures. Therefore, we borrowed some hydrodynamic principles of physics to elucidate those phenomena scientifically. Regarding the fate of the micro-anastomosed digital arteries after successful replantation, Lee et al. [38] reported that 37% of the micro-anastomosed digital arteries of replanted fingers were occluded after replantation. However, the importance of blood flow velocity in the patency rates of small vessels 1 to 2 mm in diameter has yet to be fully studied [9]. We understood why the late loss of arterial inflow to replanted fingers could be possible by observing the morphologic changes of the anastomotic microvessels in the case presented here. We believe this phenomenon could be explained by the basic physical principles of fluid dynamics. The radius of the digital artery, which was the post-anastomotic site, decreased and its wall thickness increased due to the decreased tension exerted to maintain constant exerted hydraulic pressure and homeostasis in the microvascular anastomosis site.
Besides the aforementioned basic hydrodynamic principles, there were more hemodynamic concerns yet to be resolved. Although exact time point of vascular changes after the free flap transfer is unknown, morphological changes occur in the blood flow of the flap’s pedicle and the recipient artery after 2 months from the initial surgery in our case. Depending upon the difference between the free flap anatomy or physiology, various hemodynamic changes occur. Studies on the anastomosis patterns, such as end-to-side vs. end-to-end [10,11], the type of the included flaps, muscle flaps vs. skin flaps [26-28], high vs. low volume fluid management [3], and hemodynamic changes between the donor and recipient arteries [30,32,39] in free tissue transfers are still ongoing.
In this paper, we present the possible implications of simple flow mechanics in free tissue transfer by theoretical explanations and detailed illustrations of the mechanisms of thickened and constricted lumen of the post-anastomosed pedicled recipient artery. Because only limited clinical and experimental data are available on the various changes of microvessels after free tissue transfer regarding the size of lumen and thickness of wall, further studies are needed to support the explanation of vascular changes by comparing the different measurement of velocity, pressure of blood flow, and diameter of vessels at the anastomotic site. However, by applying the simple principles of physics to microvascular anastomosis in free tissue transfer, we can understand not only the basics of the interrelationship between blood flow and hydraulic pressure, but also the morphologic changes in the anastomotic site of the microvessel.
Fig. 1.
(A, B) A 54-year-old male patient sustained a severe crushing injury to his right hand and received a middle finger ectopic replantation to make a thumb. The radial artery was anastomosed to the digital artery. (C) Two months later, he had an additional anteromedial thigh (AMT) free flap procedure to resurface the web space. After the excision of the stenotic microvessels in the previous anastomosed site, a Y-shaped vein graft was performed. (D) Postoperative 4 months view.

Fig. 2.
The radial artery was anastomosed with the digital artery for the ectopic replantation. The edge of the digital artery was bevel-cut to overcome the size discrepancy.
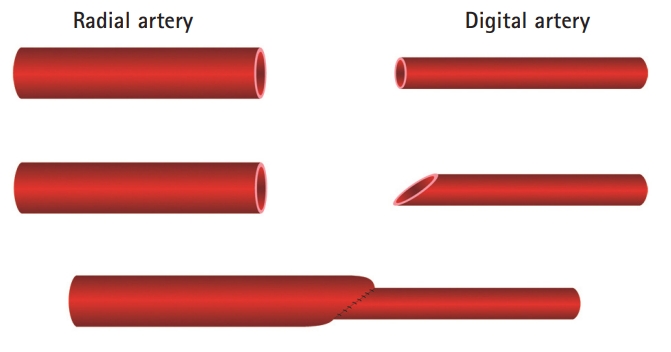
Fig. 3.
Changes in the microvessels after 2 months of microvascular anastomosis. (A) The post-anastomotic digital artery was constricted and its wall was thickened compared to the preoperative vessel. (B) The size of the vascular lumen and wall thickness were compared.
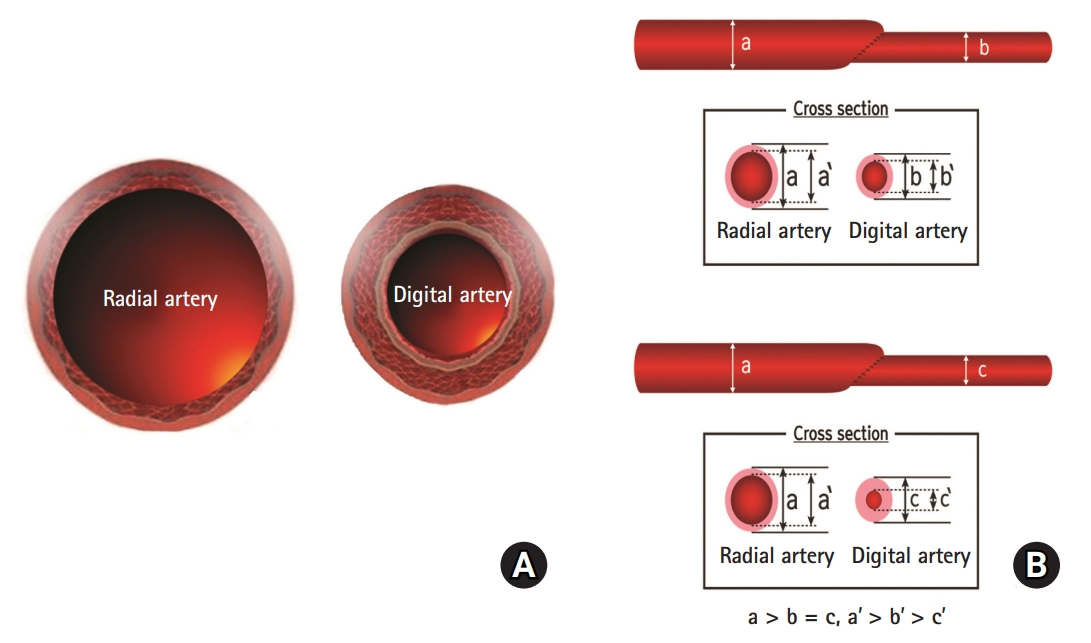
Fig. 4.
Poiseuille’s law. The blood volume flowing through a vessel is directly proportional to the pressure drop along with the distance of the vessel (P1–P2) and the fourth power of the radius of the vessel and inversely proportional to the length of the vessel (L) and the viscosity of the blood (η).
Volume flow rate (F)=
pressure difference (P1–P2)/viscous resistance (R)

Fig. 5.
Assuming that a constant amount of flow is maintained, the velocity of blood flow increases as it passes through the narrower vascular lumen.

Fig. 6.
Bernoulli’s principle. When the blood flow speeds up in a constricted vessel area, its exerted pressure is decreased in that region, assuming that the density is constant (V1<V2, P1>P2).
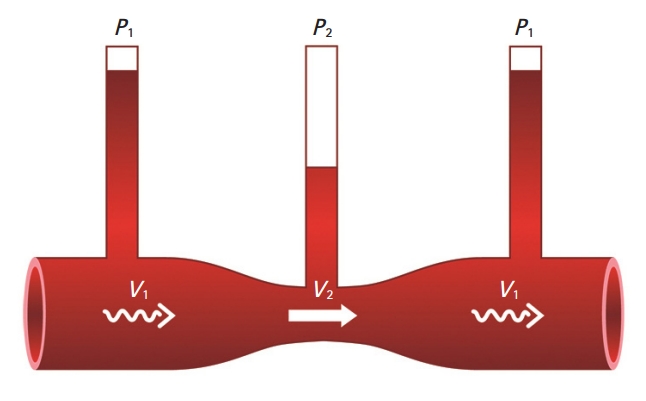
Fig. 7.
Laplace’s law. (A) Simple illustration of Laplace’s law. At constant pressure, the wall tension (T) of the vessel can be decreased simply by increasing the thickness of the vessel wall. The thicker the wall, the lower the exerted wall tension. (B) Assuming that the thickness of the vessel wall is very small compared to the diameter of the vessel lumen, its exerted pressure (P) is related to the wall tension (T) of the vessel. The wall tension is proportional to the radius (R) of the vessel for a given exerted pressure.
REFERENCES
1. Bui DT, Cordeiro PG, Hu QY, Disa JJ, Pusic A, Mehrara BJ. Free flap reexploration: indications, treatment, and outcomes in 1193 free flaps. Plast Reconstr Surg. 2007;119:2092-100.


2. Sigurdsson GH. Perioperative fluid management in microvascular surgery. J Reconstr Microsurg. 1995;11:57-65.



3. Booi DI. Perioperative fluid overload increases anastomosis thrombosis in the free TRAM flap used for breast reconstruction. Eur J Plast Surg. 2011;34:81-6.


4. Lorenzetti F, Salmi A, Ahovuo J, Tukiainen E, Asko-Seljavaara S. Postoperative changes in blood flow in free muscle flaps: a prospective study. Microsurgery. 1999;19:196-9.


5. Ichinose A, Tahara S, Terashi H, Yokoo S. Reestablished circulation after free radial forearm flap transfer. J Reconstr Microsurg. 2004;20:207-13.



6. Numata T, Iida Y, Shiba K, et al. Usefulness of color Doppler sonography for assessing hemodynamics of free flaps for head and neck reconstruction. Ann Plast Surg. 2002;48:607-12.


7. Hanasono MM, Ogunleye O, Yang JS, Hartley CJ, Miller MJ. Changes in blood velocity following microvascular free tissue transfer. J Reconstr Microsurg. 2009;25:417-24.




8. Lorenzetti F, Ahovuo J, Suominen S, Salmi A, Asko-Seljavaara S. Colour Doppler ultrasound evaluation of haemodynamic changes in free tram flaps and their donor sites. Scand J Plast Reconstr Surg Hand Surg. 2002;36:202-6.


9. Bodor R, Yoleri L, Zhang F, Buncke GM, Lineaweaver WC, Buncke HJ. Blood-flow velocity as a factor in postoperative microvascular patency. J Reconstr Microsurg. 1997;13:463-70.



10. Szilagyi DE, Whitcomb JG, Schenker W, Waibel P. The laws of fluid flow and arterial grafting. Surgery. 1960;46:55-73.
11. Miyamoto S, Takushima A, Okazaki M, Ohura N, Minabe T, Harii K. Relationship between microvascular arterial anastomotic type and area of free flap survival: comparison of end-to-end, end-to-side, and retrograde arterial anastomosis. Plast Reconstr Surg. 2008;121:1901-8.


12. Yoon AP, Jones NF. Critical time for neovascularization/angiogenesis to allow free flap survival after delayed postoperative anastomotic compromise without surgical intervention: a review of the literature. Microsurgery. 2016;36:604-12.


13. Seidenberg B, Hurwitt ES, Carton CA. The technique of anastomosing small arteries. Surg Gynecol Obstet. 1958;106:743-6.

14. O’Brien BM, Morrison WA, Ishida H, MacLeod AM, Gilbert A. Free flap transfers with microvascular anastomoses. Br J Plast Surg. 1974;27:220-30.


15. Monsivais JJ. Microvascular grafts: effect of diameter discrepancy on patency rates. Microsurgery. 1990;11:285-7.


16. In: Fieldman JS, Phong DH, Saint-Aubin Y, Vinet L, editors. Biology and mechanics of blood flows, part II: mechanics and medical aspects. New York: Springer Science+Business Media LLC; 2007. Chapter 4-2, Blood rheology; p. 119-22.
17. Taylor KJ, Holland S. Doppler US. Part I. Basic principles, instrumentation, and pitfalls. Radiology. 1990;174:297-307.


18. Zhang F, Oliva A, Kao SD, Newlin L, Buncke HJ. Microvascular vein grafts in the rat cutaneous free-flap model. J Reconstr Microsurg. 1994;10:229-33.



19. Bayramiçli M, Tetik C, Sönmez A, Gürünlüoğlu R, Baltaci F. Reliability of primary vein grafts in lower extremity free tissue transfers. Ann Plast Surg. 2002;48:21-9.


20. Darius O. The clipped microvascular anastomosis: hemodynamical, morphological and surgical evaluation. Belgium: Leuven University Press; 2004.
21. del Zoppo GJ. Virchow’s triad: the vascular basis of cerebral injury. Rev Neurol Dis. 2008;5(Suppl 1):S12-21.

22. Allan BD. Mechanism of iris prolapse: a qualitative analysis and implications for surgical technique. J Cataract Refract Surg. 1995;21:182-6.


23. Beris AE, Soucacos PN, Touliatos AS. Experimental evaluation of the length of microvenous grafts under normal tension. Microsurgery. 1992;13:195-9.


24. Recordati G. The contribution of the giraffe to hemodynamic knowledge: a unified physical principle for the circulation. Cardiologia. 1999;44:783-9.
25. Chen KT, Mardini S, Chuang DC, et al. Timing of presentation of the first signs of vascular compromise dictates the salvage outcome of free flap transfers. Plast Reconstr Surg. 2007;120:187-95.


26. Siemionow M, Andreasen T, Chick L, Lister G. Effect of muscle flap denervation on flow hemodynamics: a new model for chronic in vivo studies. Microsurgery. 1994;15:891-4.


27. Lorenzetti F, Giordano S, Tukiainen E. Intraoperative hemodynamic evaluation of the latissimus dorsi muscle flap: a prospective study. J Reconstr Microsurg. 2012;28:273-8.



28. Chen LE, Seaber AV, Bossen E, Urbaniak JR. The effect of acute denervation on the microcirculation of skeletal muscle: rat cremaster model. J Orthop Res. 1991;9:266-74.


29. Nasir S, Baykal B, Altuntaş S, Aydin MA. Hemodynamic differences in blood flow between free skin and muscles flaps: prospective study. J Reconstr Microsurg. 2009;25:355-60.



30. Kurita M, Takushima A, Shiraishi T, Okazaki M, Ozaki M, Harii K. Alteration of arterial blood flow after free muscle transfer. Ann Plast Surg. 2010;64:477-81.


31. Lorenzetti F, Giordano S, Suominen E, Asko-Seljavaara S, Suominen S. Intraoperative hemodynamic evaluation of the radial and ulnar arteries during free radial forearm flap procedure. J Reconstr Microsurg. 2010;26:73-7.



32. Lorenzetti F, Kuokkanen H, von Smitten K, Asko-Seljavaara S. Intraoperative evaluation of blood flow in the internal mammary or thoracodorsal artery as a recipient vessel for a free TRAM flap. Ann Plast Surg. 2001;46:590-3.


33. Nasir S, Aydin MA, Sonmez E, Baykal B. Flow-through free latissimus dorsi flap for reconstruction of injured limbs: evaluation of hemodynamic effects on extremity circulation. Ann Plast Surg. 2010;65:164-9.


34. Cooley BC, Lan M, Gould JS. Rat femoral vein-to-vein grafts as a microvascular practice model: factors that influence patency. Microsurgery. 1991;12:43-5.


36. Fujikawa S, O'Brien BM. An experimental evaluation of microvenous grafts. Br J Plast Surg. 1975;28:244-6.


37. Salgado CJ, Smith A, Kim S, et al. Effects of late loss of arterial inflow on free flap survival. J Reconstr Microsurg. 2002;18:579-84.



-
METRICS

-
- 2 Crossref
- 3,105 View
- 79 Download
- Related articles in Arch Hand Microsurg
-
Sensory Function Recovery by Free Tissue Transfer in the Extremities2005 May;14(1)






